In this project we will be implementing the KNN algorithm from scratch. We will implement the algorithm for the K values 1, 3, 5 and 7 and see which one is performing better. Also, we will implement multiple distance measures and compare accurac across all of them.
We begin by importing the necessary libraries
1import math23import matplotlib.pyplot as mp4import numpy as np5import pandas as pd
1DATA = "../data/iris.data"2SPLIT_PERCENT = 0.73K_VALUES = [1, 3, 5, 7]4DIST_METRICS = ["euc", "norm-euc", "cosine-sim"]
We now prepare the dataset for further processing. To do this we first load the data, shuffle it randomly and map the classes to integers for easier processing
1dataset = pd.read_csv(DATA).sample(frac=1).reset_index(drop=True)23# Map class names to integers4iris_class_map = {v: k + 1 for k, v in enumerate(dataset['class'].unique())}5dataset['class'] = dataset['class'].map(iris_class_map)67RECORDS_COUNT, ATTR_COUNT = dataset.shape8ATTRS = dataset.columns.values[0:ATTR_COUNT - 1]9SPLIT_SIZE = math.floor(RECORDS_COUNT * SPLIT_PERCENT)1011# List of columns for every K Value12K_COL_STRINGS = ["pred_k_{}".format(k) for k in K_VALUES]13for col in K_COL_STRINGS:14 dataset[col] = np.nan1516# Split dataset for dev and test17dev_set = dataset[:SPLIT_SIZE].copy(deep=True)18test_set = dataset[SPLIT_SIZE:].copy(deep=True)1920print("Dev data")21dev_set.head()
1Dev data
| sepal_len | sepal_wid | petal_len | petal_wid | class | pred_k_1 | pred_k_3 | pred_k_5 | pred_k_7 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.0 | 3.6 | 1.4 | 0.2 | 1 | NaN | NaN | NaN | NaN |
| 1 | 7.0 | 3.2 | 4.7 | 1.4 | 2 | NaN | NaN | NaN | NaN |
| 2 | 6.8 | 2.8 | 4.8 | 1.4 | 2 | NaN | NaN | NaN | NaN |
| 3 | 5.7 | 2.8 | 4.1 | 1.3 | 2 | NaN | NaN | NaN | NaN |
| 4 | 5.5 | 2.4 | 3.8 | 1.1 | 2 | NaN | NaN | NaN | NaN |
Now that our data is prepared, we need to find the nearest neighbors for every K value. To do this, we first need to calculate the Euclidian distance for every row in the dev set against every other row. Once we have the distances, we find the K Nearest Neighbors for every K value and use this to predict the class of the selected vector.
Once we make our predictions, we need to calculate the accuracy as well.
1# Find K nearest neighbors for all values of K2for index, k in enumerate(K_VALUES):3 calculated_pred = []4 for i, row in dev_set.iterrows():5 # Calculate euclidian distance6 calculated_dist = (dev_set[ATTRS].sub(row[ATTRS]).pow(2).sum(1).pow(0.5)).sort_values()7 # Get indices of nearest neighbors8 nearest_neighbor_indices = calculated_dist.iloc[0:k].index.values9 # Get nearest neighbors10 nearest_neighbors = dev_set.loc[nearest_neighbor_indices, :]['class']11 # Predict class of the vector12 prediction = nearest_neighbors.mode().values[0]13 calculated_pred.append(prediction)14 dev_set[K_COL_STRINGS[index]] = calculated_pred1516# Calculating accuracy17euc_accuracy = []1819for col in dev_set[K_COL_STRINGS]:20 column = dev_set[col]21 total_rows = dev_set.shape[0]22 num = dev_set.loc[dev_set['class'] == column].shape[0]23 acc = round((num/total_rows) * 100, 5)24 euc_accuracy.append(acc)2526print(euc_accuracy)
1[100.0, 99.04762, 99.04762, 98.09524]
Now, follow the same process but instead we use a normalized euclidian distance as a metric. To do this, we normalize the dataset and calculate the euclidian distance again. This allows us to deal with outliers and ensure we are correctly scaling the data
1# Normalize data2def normalize(dataframe):3 df = dataframe.copy(deep=True)4 for col in df[ATTRS]:5 df[col] = (df[col] - df[col].min()) / (df[col].max() - df[col].min())6 return df78norm_dev_set = normalize(dev_set)910# Reset the prediction columns11for col in K_COL_STRINGS:12 norm_dev_set[col] = np.nan1314norm_dev_set.head()
| sepal_len | sepal_wid | petal_len | petal_wid | class | pred_k_1 | pred_k_3 | pred_k_5 | pred_k_7 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.194444 | 0.842105 | 0.067797 | 0.043478 | 1 | NaN | NaN | NaN | NaN |
| 1 | 0.750000 | 0.631579 | 0.627119 | 0.565217 | 2 | NaN | NaN | NaN | NaN |
| 2 | 0.694444 | 0.421053 | 0.644068 | 0.565217 | 2 | NaN | NaN | NaN | NaN |
| 3 | 0.388889 | 0.421053 | 0.525424 | 0.521739 | 2 | NaN | NaN | NaN | NaN |
| 4 | 0.333333 | 0.210526 | 0.474576 | 0.434783 | 2 | NaN | NaN | NaN | NaN |
Once the dataset is normalized, we follow the same process to calculate the euclidian distance and predict
1# Predict using normalized data for all K values2for index, k in enumerate(K_VALUES):3 calculated_pred = []4 for i, row in norm_dev_set.iterrows():5 calculated_dist = (norm_dev_set[ATTRS].sub(row[ATTRS]).pow(2).sum(1).pow(0.5)).sort_values()6 nearest_neighbor_indices = calculated_dist.iloc[0:k].index.values7 nearest_neighbors = norm_dev_set.loc[nearest_neighbor_indices, :]['class']8 prediction = nearest_neighbors.mode().values[0]9 calculated_pred.append(prediction)10 norm_dev_set[K_COL_STRINGS[index]] = calculated_pred1112norm_euc_accuracy = []1314for col in norm_dev_set[K_COL_STRINGS]:15 column = norm_dev_set[col]16 total_rows = norm_dev_set.shape[0]17 num = norm_dev_set.loc[dev_set['class'] == column].shape[0]18 acc = round((num/total_rows) * 100, 5)19 norm_euc_accuracy.append(acc)2021print(norm_euc_accuracy)
1[100.0, 98.09524, 99.04762, 99.04762]
For the final iteration, we will use Cosine Similarity as a distance metric
1# Dot product2def dot(A, B):3 return sum(a * b for a, b in zip(A, B))45# Cosine Similarity6def cosine_similarity(a, b):7 return 1 - dot(a, b) / ((np.sqrt(dot(a, a))) * (np.sqrt(dot(b, b))))89cosine_dev_set = dev_set.copy(deep=True)1011for index, k in enumerate(K_VALUES):12 calculated_pred = []13 for i, row in cosine_dev_set.iterrows():14 calculated_dist = cosine_dev_set[ATTRS].apply(lambda a: cosine_similarity(np.array(a), np.array(row[ATTRS])), axis=1).sort_values()15 nearest_neighbor_indices = calculated_dist.iloc[0:k].index.values16 nearest_neighbors = cosine_dev_set.loc[nearest_neighbor_indices, :]['class']17 prediction = nearest_neighbors.mode().values[0]18 calculated_pred.append(prediction)19 cosine_dev_set[K_COL_STRINGS[index]] = calculated_pred2021cosine_accuracy = []2223for col in cosine_dev_set[K_COL_STRINGS]:24 column = cosine_dev_set[col]25 total_rows = cosine_dev_set.shape[0]26 num = cosine_dev_set.loc[dev_set['class'] == column].shape[0]27 acc = round((num/total_rows) * 100, 5)28 cosine_accuracy.append(acc)2930print(cosine_accuracy)
1[100.0, 98.09524, 98.09524, 99.04762]
Now, we need to analyze the accuracy of all these distance metrics across all the K values and pick the one that's doing the best job. To do this
1acc_table = pd.DataFrame(index=K_VALUES)2acc_table[DIST_METRICS[0]] = euc_accuracy3acc_table[DIST_METRICS[1]] = norm_euc_accuracy4acc_table[DIST_METRICS[2]] = cosine_accuracy5acc_table
| euc | norm-euc | cosine-sim | |
|---|---|---|---|
| 1 | 100.00000 | 100.00000 | 100.00000 |
| 3 | 95.23810 | 95.23810 | 98.09524 |
| 5 | 96.19048 | 95.23810 | 98.09524 |
| 7 | 98.09524 | 96.19048 | 98.09524 |
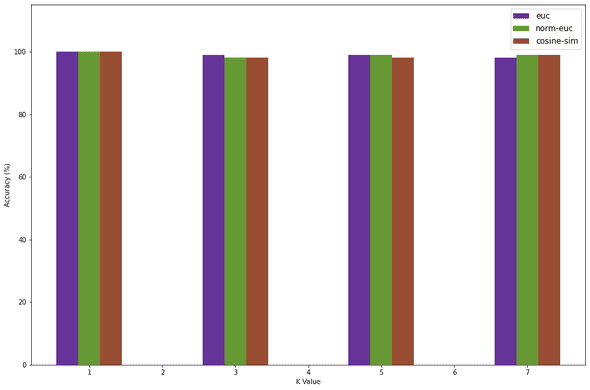
1width = 0.32mp.figure(figsize=(15, 10))3mp.ylim(0, 115)4e = mp.bar(x=np.add(K_VALUES, width * -1), height=euc_accuracy, width=width, color='#663399')5n = mp.bar(x=np.add(K_VALUES, width * 0), height=norm_euc_accuracy, width=width, color='#669933')6c = mp.bar(x=np.add(K_VALUES, width * 1), height=cosine_accuracy, width=width, color='#994d33')78mp.legend(DIST_METRICS, loc="best", fontsize=12)9mp.xlabel("K Value")10mp.ylabel("Accuracy (%)")11mp.show()
We see that at K = 1, we get 100% accuracy. This is mainly because overfitting is occuring. From my observations K values 3 and 5 seem to be most stable and the accuracy for K = 7 usually decreases. This is why I will be choosing K = 3 and the Normalized Euclidian distance since it is stable to test the accuracy of the test dataset.
1k_val = 32norm_test_set = normalize(test_set)34calculated_pred = []5for i, row in norm_test_set.iterrows():6 calculated_dist = (norm_test_set[ATTRS].sub(row[ATTRS]).pow(2).sum(1).pow(0.5)).sort_values()7 nearest_neighbor_indices = calculated_dist.iloc[0:k_val].index.values8 nearest_neighbors = norm_test_set.loc[nearest_neighbor_indices, :]['class']9 prediction = nearest_neighbors.mode().values[0]10 calculated_pred.append(prediction)11norm_test_set[K_COL_STRINGS[1]] = calculated_pred1213norm_euc_accuracy = []1415column = norm_dev_set[K_COL_STRINGS[1]]16total_rows = norm_dev_set.shape[0]17num = norm_dev_set.loc[dev_set['class'] == column].shape[0]18acc = round((num/total_rows) * 100, 5)19norm_euc_accuracy.append(acc)2021print(norm_euc_accuracy)
1[98.09524]
The final accuracy we get on the test set is around ~98% which is pretty good
The notebook can be downloaded here if you'd like to review it
References:
Develop k-Nearest Neighbors in Python From Scratch - Machine Learning Mastery